Imagine you're facing a wall that stretches forever off in either direction. We all know that the further parts of the wall look smaller than the closer parts. That's called "perspective". We tend to imagines lines of perspective aiming straight toward some distant point, but in fact they don't.

Consider this image:

If the perspective lines aimed straight at some point, the wall wouldn't disappear at that point -- it would flip upside down and eventually appear infinitely tall. Clearly, perspective lines curve as they get farther away so that they never actually quite meet. Here's an eggagerated picture:

If that's what the wall looks like to the left and right, what do the lines look like when they meet directly in front of you? If the persepective lines continued to curve away from each other as they got closer (concave outward), the wall would look like this:

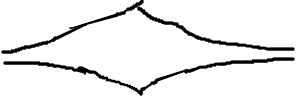
That's obviously wrong. So it must look something like this:

If that's the case, then at some point, the perspective lines must go from being concave outward to being concave inward. At what point does that happen? I'm a little too busy (or is it lazy?) to check the math right now, but I think it did it once a long time ago when I first considered this question and found that the "inflection points" occur either the same distance down the wall to either side as the distance between you and the wall, or at the point where the distance from your eye to the wall is the same as the distance from point on the wall directly in front of your eye to the top or bottom of the wall.

If the latter is correct, then the top and bottom inflection points could be different distances down the wall if your eye isn't at half the height of the wall.

When we look at objects, we don't notice this curvature of the image being cast on our eyes. Part of the reason may be that the curvature is slight enough that it's not very noticable. But a bigger reason may be simply that we know that the objects are straight, so our brains have learned to mentally "correct" the curvature (similar to how when we look at a door from and angle, we still see it as a rectangle, even though the actual shape of the image being cast on our retina is more like a trapezoid or parallelogram).

Reader Comment:
Antone Roundy said:
Sandra, I just found your comment, not yet moderated in the queue. Think of it this way -- what if you encountered an infinitely long wall floating in space. There'd be no horizon for the top and the bottom of the wall to meet at. Or conside...
(join the conversation below)

If you look at a "fish eye lens" photo or a 360 degree photo, you'll notice the curvature, because those photo techniques make it more pronounced.

I suspect that when a skilled artist paints an object, they curve their perspective lines, because they have learned to tune out the part of their mind that identifies objects and tells them what shape they ought to be, and instead simply paint the light that is entering their eyes. (For more about that, and how to learn to do it, I recommend Drawing on the Right Side of the Brain, by Betty Edwards).